Question

You analyze a sample of a meteorite that landed on Earth and find that 15/16 of a certain type of radioactive atoms have decayed into the corresponding daughter atom. Calculate the number of half-lives that have occurred.

Answer 1

The number of half-lives that have occurred are 4.

Step-by-step explanation:

Formula used for number of half lives :

`a=(a_o)/(2^n)`

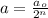
where,

a = amount of reactant left after n-half lives

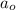`a_o` = Initial amount of the reactant

n = number of half lives

`a_o=x`

`a = x-(15)/(16)x=(1)/(16)x=a`

`(1)/(16)x=(x)/(2^n)`

`2^n=16=2^4`

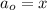
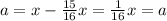
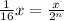
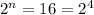
n = 4

The number of half-lives that have occurred are 4.