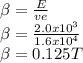Question

A proton travelling to the right with horizontal speed 1.6×10 4ms –1 enters a uniform electric field of strength E. The electric field has magnitude 2.0×10 3NC –1 and is directed downwards. Calculate the magnitude of the electric force acting on the proton when it is in the electric field.

Answer 1

F=
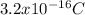`3.2x10^(-16)C`[/tex]

β=0.125 T

Step-by-step explanation:

E=
`2.0x10^(3)`
`(N)/(C)`

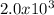
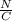
ve=
`1.6x10^(4) (m)/(s)`

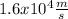
Proton charge q=
`1.6x10^(-19) C`

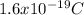
The magnitude of the electric force acting on the proton when it is in the electric field

Is equal to the velocity of the proton traveling by the electric field so:

`F=q*E \\F=1.6x10^(-16)C*2.0x10^(3)(N)/(C) \\F=3.2x10^(-16) N`

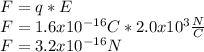
The magnitude of the field is

`\beta =(E)/(ve)\\\beta=(2.0x10^(3))/(1.6x10^(4)) \\\beta=0.125 T`