Question

An uncrewed mission to the nearest star, Proxima Centauri, is launched from the Earth's surface as a projectile with an initial speed of 44.4 km/s, just enough for the spacecraft to escape the Earth's gravity and leave the solar system. Ignoring air resistance and the Earth's rotation, what is the speed of the spacecraft when it is more than halfway to the star? Assume we are ignoring the effect of the Sun on the spacecraft.

Answer 1

42.96 km/s

Step-by-step explanation:

From the conservation of Energy

`(PE+KE)_i=(PE+KE)_f\\\Rightarrow -(GmM)/(R)+(1)/(2)mv_i^2=0+(1)/(2)mv_f^2`

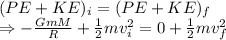
Mass gets cancelled

`-(GM)/(R)+(1)/(2)v_i^2=0+(1)/(2)v_f^2\\\Rightarrow -2(GM)/(R)+v_i^2=v_f^2\\\Rightarrow -v_e^2+v_i^2=v_f^2\\\Rightarrow v_f=√(v_i^2-v_e^2)`

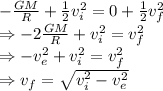
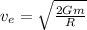`v_e=\sqrt{(2Gm)/(R)}` = Escape velocity of Earth = 11.2 km/s

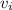`v_i` = Velocity of projectile = 44.4 km/s

`v_f=√(44.4^2-11.2^2)\\\Rightarrow v_f=42.96\ km/s`

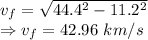
The velocity of the spacecraft when it is more than halfway to the star is 42.96 km/s