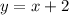1 Answer

Srivats Shankar · Answer 1 · 2020-08-13T22:12:41+0000

The required equation is y = x + 2

Solution:

Given three points are (1,3) (3,5) (5,7)

A quadratic equation for three points is given by
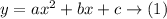
$y = ax^2 + bx + c \rightarrow (1)$

Assume the point 1,3 and substitute in (1)

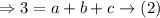
$\Rightarrow 3= a + b + c \rightarrow (2)$

Let us substitute 3,5 in (1)

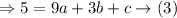
$\Rightarrow 5 = 9a + 3b + c \rightarrow (3)$

Let us substitute 5,7 in (1)

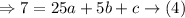
$\Rightarrow 7 = 25a + 5b + c \rightarrow (4)$

Subtracting 2 and 3

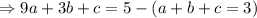
$\Rightarrow 9a + 3b + c = 5 - ( a+ b+ c = 3)$

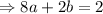
$\Rightarrow 8a + 2b = 2$

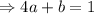
$\Rightarrow 4a + b = 1$

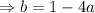
$\Rightarrow b = 1-4a$

Subtracting 4 and 3

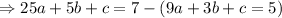
$\Rightarrow 25a + 5b + c = 7 - ( 9a + 3b + c = 5)$

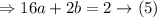
$\Rightarrow 16a + 2b = 2 \rightarrow (5)$

Substituting b in 5,
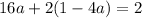
16a + 2(1 -4a) = 2

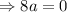
$\Rightarrow 8a = 0$

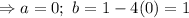
$\Rightarrow a = 0; \ b = 1- 4(0) = 1$

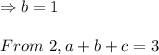
$\Rightarrow b = 1 \\\\From \ 2, a + b + c =3$

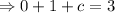
$\Rightarrow 0+1+c =3$

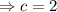
$\Rightarrow c = 2$

Substituting a, b, c in 1 we get the quadratic equation
y = x + 2

Please log in or register to add a comment.