Question

A random sample of 85 adults found that the average calorie consumption was 2100 per day. Previous research has found a standard deviation of 450 calories, and you use this value for \sigma σ. A researcher wants to estimate a 95% confidence interval and is willing to accept a margin of error of \pm 50 ± 50 calories. She knows it will cost $50 to survey each member of the sample. Given this information, how much will it cost to survey the minimum number of people?

Answer 1

$15600

Explanation:

Minimum number of samples can be calculated using the formula:

N≥
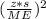`((z*s)/(ME))^2` where

• N is the sample size
• z is the corresponding z-score for 95% confidence level (1.96)
• s is the standard deviation of the calorie consumption (450 cal.)
• ME is the margin of error that the researcher is willing to accept. (50 cal)

N≥
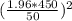`((1.96*450)/(50))^2` =311.2

Therefore, minimum required sample size for 50 cal standard error in 95% confidence is 312

Since the survey costs $50 for each person then the survey costs minimum

50*312=$15600