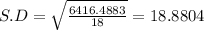Question

In a data analysis, the breakdown time of an insulating fluid between electrodes at 34 kV is recorded. The times, in minutes, are as follows: 0.19, 0.78, 0.96, 1.31, 2.78, 3.16, 4.15, 4.67, 4.85, 6.50, 7.35, 8.01, 8.27, 12.06, 31.75, 32.52, 33.91, 36.71, and 72.89. Calculate the sample mean and sample standard deviation

Answer 1

To calculate the sample mean, add up the values and divide by the total number of values. For the given dataset, the sample mean is 8.54 minutes. To calculate the sample standard deviation, find the squared differences from the mean, sum them up, divide by the total number of values minus 1, and take the square root. The sample standard deviation is approximately 5.225 minutes.

Step-by-step explanation:

To calculate the sample mean, you need to sum up all of the values in the dataset and then divide by the total number of values. For the given dataset, the sum of the breakdown times is 162.15, and there are 19 values. Therefore, the sample mean is 162.15 / 19 = 8.54 minutes.

To calculate the sample standard deviation, you need to find the difference between each value and the mean, square the differences, sum them up, divide by the total number of values minus 1, and then take the square root of the result. The sum of the squared differences is 491.4235, so the sample variance is 491.4235 / (19-1) = 27.3013. Finally, the sample standard deviation is the square root of the sample variance, which is approximately 5.225 minutes.

Answer 2

Sample mean = 14.3589

Sample standard deviation = 18.8804

Step-by-step explanation:

We are given the following information:

0.19, 0.78, 0.96, 1.31, 2.78, 3.16, 4.15, 4.67, 4.85, 6.50, 7.35, 8.01, 8.27, 12.06, 31.75, 32.52, 33.91, 36.71, 72.89

Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

where
`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(272.82)/(19) = 14.3589`

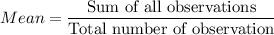
Sum of squares of differences = 200.7590696 + 184.3878117 + 179.5317906 + 170.2750275 + 134.0720222 + 125.4164222 + 104.2226064 + 93.8757011 + 90.42008005 + 61.76305373 + 49.12534321 + 40.30913268 + 37.07528005 + 5.285159001 + 302.4487116 + 329.8238326 + 382.2436589 + 499.5695537 + 3425.884122 = 6416.4883

`S.D = \sqrt{(6416.4883)/(18)} = 18.8804`