Answer:
C. 3.74 g/L
Step-by-step explanation:
Using ideal gas equation as:
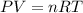
where,
P is the pressure
V is the volume
n is the number of moles
T is the temperature
R is Gas constant having value = 0.0821 L.atm/K.mol
Also,
Moles = mass (m) / Molar mass (M)
Density (d) = Mass (m) / Volume (V)
So, the ideal gas equation can be written as:
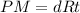
At STP,
Pressure = 1 atm
Temperature = 273.15 K
Molar mass of krypton gas = 83.8 g/mol
Applying the equation as:
1 atm × 83.8 g/mol = d × 0.0821 L.atm/K.mol × 273.15 K
⇒d = 3.74 g/L