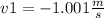Question

The recoil of a shotgun can be significant. Suppose a 3.6-kg shotgun is held tightly by an arm and shoulder with a combined mass of 15.0 kg. Part A When the gun fires a projectile with a mass of 0.049 kg and a speed of 380 m/s, what is the recoil velocity of the shotgun and arm–shoulder combination? Express your answer to three significant figures and include appropriate units.

Answer 1

The recoil velocity of the shotgun and arm-shoulder combination is
`-1.001(m)/(s)`

Step-by-step explanation:

To solve this problem we are going to use the momentum conservation principle.

The total linear momentum of an isolated system remains constant if the sum of the exterior forces is zero. In this case, the sum of the exterior forces is zero. Therefore we can use this principle.

The equation that we are going to use is :

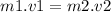`m1.v1=m2.v2` (I)

Where m1 is the mass of the shotgun and arm-shoulder combination.

Where v1 is the recoil velocity of the system formed by shotgun and arm-shoulder combination.

Where m2 is the mass of the projectile.

And where v2 is the velocity of the projectile.

The mass of the system formed by shotgun and arm-shoulder combination is the sum between the mass of the shotgun and the mass of the arm-shoulder combination.

If we replace all the data in the equation (I) :

`(3.6kg+15.0kg).v1=(0.049kg).(380(m)/(s))`

`v1=((0.049kg).(380(m)/(s)))/((3.6kg+15.0kg))=1.001(m)/(s)`

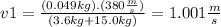
Now, if we consider as positive the sense of the projectile's velocity the sense of the system's velocity formed by the shotgun and the arm-shoulder combination will be negative (because is the opposite sense).

We finalize adding a negative sign to the velocity :

`v1=-1.001(m)/(s)`

Answer 2

The velocity of the recoil is
`v=1.001 (m)/(s)`

Step-by-step explanation:

Kinetic Energy

`m_(bullet)*v_(bullet)=m_(gun)*v_(recoil)\\m_(gun)= 15.0kg+3.6kg`

The mass of th gun is the both mass the shotgun and the arm shoulder combination

`m_(bullet)=0.049kg\\v_(bullet)=380(m)/(s) \\m_(bullet)*v_(bullet)=m_(gun)*v_(recoil)\\0.049kg*380(m)/(s)=(15.kg+3.6kg)* v_(recoil)\\v_(recoil)=-(18.62 kg (m)/(s) )/(18.6 kg)\\ v_(recoil)=-1.0010 (m)/(s)`

The velocity is negative because is in opposite direction of the bullet