Question

Solve the Law of Cosine: c^2 = a^2+ b^2 - 2abcosC for cos C.

Answer 1

a on ed

Explanation:

Answer 2

The Law of Cosine : cos C =
`(a^(2)+ b^(2)-c^(2))/(2ab)`

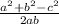
Explanation:

See the figure to understand the proof :

Let A Triangle ABC with sides a,b,c,

Draw a perpendicular on base AC of height H meet at point D

Divide base length b as AD = x -b and CD = x

By Pythagoras Theorem

In Triangle BDC And In Triangle BDA

a² = h² + x² ( 1 ) c² = h² + (x-b)²

c² = h² + x² + b² - 2xb ...(. 2)

From above eq 1 and 2

c² = (a² - x²) + x² + b² - 2xb

or, c² = a² + b² - 2xb .....(3)

Again in ΔBDC

cos C =
`(BD)/(BC)`

Or, cos C =
`(x)/(a)`

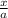
∴ x= a cos C

Now put ht value of x in eq 3

I.e, c² = a² + b² - 2ab cos C

Hence , cos C =
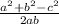`(a^(2)+ b^(2)-c^(2))/(2ab)` Proved Answer