Answer: 2.093
Explanation:
As per give , we have
Sample size : n= 20
Degree of freedom : df= n-1=19
Significance level :
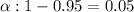
Since , the sample size is small (n<30) so we use t-test.
For confidence interval , we find two-tailed test value.
Using students's t-critical value table,
Critical t-value :
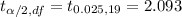
Thus, the critical value for the 95% confidence interval = 2.093