Question

After hitting the spring, the block is bounced back up the ramp. The maximum compression of the spring is Δx=0.03m, and the spring constant is k=800N/m. What is the velocity of the block when it first reaches a height of 0.1m above the ground on the ramp? The mass of the block is m=0.2kg, take g=9.8m/s^2 .

Answer 1

v = 1.28 m/s

Step-by-step explanation:

Given that,

Maximum compression of the spring,
`\Delta x=0.03\ m`

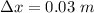
Spring constant, k = 800 N/m

Mass of the block, m = 0.2 kg

To find,

The velocity of the block when it first reaches a height of 0.1 m above the ground on the ramp.

Solution,

When the block is bounced back up the ramp, the total energy of the system remains conserved. Let v is the velocity of the block such that,

Initial energy = Final energy

`(1)/(2)kx^2=mgh+(1)/(2)mv^2`

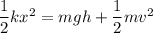
Substituting all the values in above equation,

`(1)/(2)* 800* 0.03^2=0.2* 9.8* 0.1+(1)/(2)* 0.2* v^2`

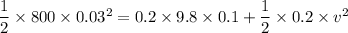
v = 1.28 m/s

Therefore the velocity of block when it first reaches a height of 0.1 m above the ground on the ramp is 1.28 m/s.