Question

A particle moves in the xy plane with constant acceleration. At time zero, the particle is at x = 6.0 m, y = 10.0 m, and has velocity v = 1.0 m/s î + 6.0 m/s ĵ. The acceleration is given by the vector a = 5.0 m/s2 î + 7 m/s2 ĵ.

(a) Find the velocity vector at t = 10.0 s.
(b) Find the position vector at t = 1.0 s.
(c) Give the magnitude and direction of the position vector in part (b).

Answer 1

Step-by-step explanation:

Given that,

Position of the particle at t = 0,

`y=(6i+10j)\ m`

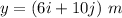
Velocity of the particle at t = 0

`u=(1i+6j)\ m`

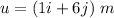
Acceleration of the particle,

`a=(5i+7j)\ m/s^2`

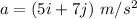
Solution,

(a) Let v is the velocity at t = 10 s. Using the equation of kinematics as :

`v=u+at`

`v=(1i+6j)+(5i+7j)10`

`v=(51i+76j)\ m/s`

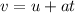
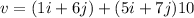
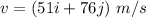
(b) Let y' is the position at t = 1 s. Again using second equation of kinematics as :

`y'=y+ut+(1)/(2)at^2`

`y'=(6i+10j)+(1i+6j)1+(1)/(2)* (5i+7j)1^2`

`y'=(19)/(2)i+(39)/(2)j`

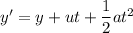
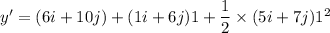
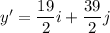
(c) Magnitude of y',

`|y'|=\sqrt{((19)/(2))^2+((39)/(2))^2}`

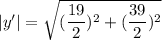
|y'| = 21.69 meters

Direction of the y',

`tan\theta=(y)/(x)`

`tan\theta=(39/2)/(19/2)`

`\theta=64.02^(\circ)`

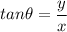
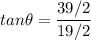
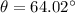
Hence, this is the required solution.