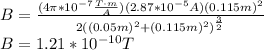Question

A nonconducting ring with a radius of 11.5 cm is uniformly charged with a total positive charge of 10.0 µC. The ring rotates at a constant angular speed of 18.0 rad/s about an axis through its center, perpendicular to the plane of the ring. What is the magnitude of the magnetic field on the axis of the ring 5.00 cm from its center?

Answer 1

`B=1.21*10^(-10)T`

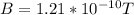
Step-by-step explanation:

The magnitude of the magnetic field on the axis of the ring is given by:

`B=\frac{\mu_0 IR^2}{2(r^2+R^2)^{(3)/(2)}}(1)`

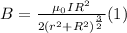
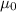`\mu_0` is the permeability of free space,
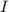`I` is the flowing current through the ring,
`R` is the ring's radius and
`r` is the distance to the center of the ring.

The flowing current through the ring is defined as the ring's charge divided into the time taken by the charge to complete one revolution, that is, the period
`T=(2\pi)/(\omega)`. So, we have:

`I=(q)/(T)\\I=(q)/((2\pi)/(\omega))\\\\I=(\omega q)/(2\pi)\\I=(18(rad)/(s)(10*10^(-6)C))/(2\pi)\\I=2.87*10^(-5)A`

Now, replacing in (1):

`B=\frac{(4\pi*10^(-7)(T\cdot m)/(A))(2.87*10^(-5)A)(0.115m)^2}{2((0.05m)^2+(0.115m)^2)^{(3)/(2)}}\\B=1.21*10^(-10)T`