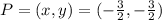Answer:
The coordinates of
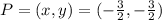
Explanation:
Coordinates of A= (1,6) and B = (-2,-3)
AP:PB = 5:1
Let the coordinates of P =(x,y)
Now, by SECTION FORMULA:
If m1: m2 is the ratio between two segments, then the coordinate of point is given as
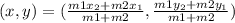
Similarly here, (x1, y1) = (1,6) , (x2, y2) = (-2,-3) and m1: m2 = 5: 1
Putting all values in equation, we get:
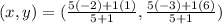
or,

Hence, the coordinates of