Question

The point-slope form of the equation of the line that passes through (–5, –1) and (10, –7) is y plus 7 equals negative StartFraction 2 over 5 EndFraction left-parenthesis x minus 10 right-parenthesis.. What is the standard form of the equation for this line?

2x – 5y = –15
2x – 5y = –17
2x + 5y = –15
2x + 5y = –17

Answer 1

C

Explanation:

Answer 2

For this case we have that by definition, the standard form of a linear equation is:

`ax + by = c`

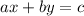
We have the following equation of the point-slope form:

`y + 7 = - \frac {2} {5} (x-10)`

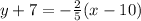
We manipulate the equation algebraically to convert it to the standard form:

We apply distributive property to the terms within parentheses, taking into account that:

`- * + = -\\- * - = +\\y + 7 = - \frac {2} {5} x + \frac {2} {5} (10)\\y + 7 = - \frac {2} {5} x + 4`

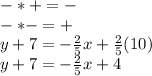
We subtract 4 from both sides of the equation:

`y + 7-4 = -\frac {2} {5}x\\y + 3 = - \frac {2} {5}x`

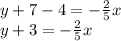
We multiply by 5 on both sides of the equation:

`5 (y + 3) = - 2x\\5y + 15 = -2x`

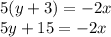
Adding 2x to both sides of the equation:

`2x + 5y + 15 = 0`

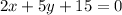
Subtracting 15 from both sides of the equation:
`2x + 5y = -15`

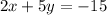
Thus, the standard form of the equation is:
`2x + 5y = -15`

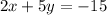
Answer:

Option C