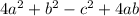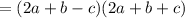Question

Factor completely: 4a^2+b^2−c^2+4ab

Answer 1

The answer above has the correct explanation but a calculation mistake. Up to the part where it simplifies to
`(2a-b)^(2) - c^(2)`, everything is right.

Using the formula (a+b) (a-b), we get (2a-b-c)(2a-b+c). Not (2a+b-c) (2a+b+c)

So, the correct answer should be: (2a - b + c) (2a - b - c)

Answer 2

`4a^(2) + b^(2)  - c^(2)  + 4ab`
`= (2a + b -c) (2a + b+c)`

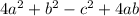
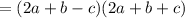
Explanation:

Here, the given expression is
`4a^(2) + b^(2)  - c^(2)  + 4ab`

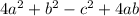
or, the given expression can be written as

`(4a^(2) + b^(2)  + 4ab ) - c^(2)`

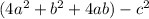
Now, by ALGEBRAIC IDENTITY:
`(x+y)^(2)  = x^(2) + y^(2)  + 2xy`

So, similarly here,
`(2a +b){2}  = 4a^(2) + b^(2)  + 4ab`

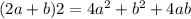
Hence, on simplification, the expression

`(4a^(2) + b^(2)  + 4ab ) - c^(2) = (2a + b)^(2) - c^(2)`

Now, by ALGEBRAIC IDENTITY:
`(x +y)(x-y) = x^(2)  - y^(2)`

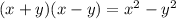
So, similarly
`(2a + b)^(2) - c^(2)`
`= (2a + b -c) (2a + b+c)`

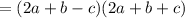
Hence, the given expression is factorized as:

`4a^(2) + b^(2)  - c^(2)  + 4ab`
`= (2a + b -c) (2a + b+c)`