Answer:
Alberto is incorrect. Perimeter is 42 units.
Explanation:
Given:
The vertices of the triangle are

Perimeter of a triangle of length
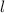 and width
and width
 is given as:
is given as:
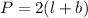
Here,
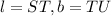
Distance between two points
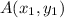 and
and
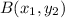 is given as:
is given as:

So, the length ST is,
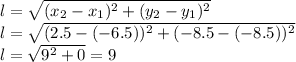
Width TU is,
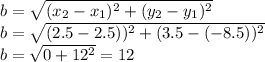
Therefore, the perimeter is given as:
Perimeter =
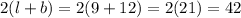 units.
units.
Hence, the perimeter written by Alberto is incorrect as perimeter is not 18 units bu 42 units.