Answer:
Only for the value of x = -9 i, f(x) = g(x)
Explanation:
Here,
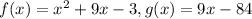
Now, find the values of the given functions:
A) at x = -9
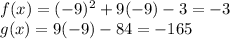
⇒ f(-9) ≠ g(-9)
B) at x = -9i
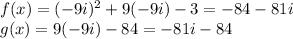
⇒ f(-9i) = g(-9i)= -84 - 81i
C) at x = -3
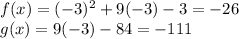
⇒ f(-3) ≠ g(-3)
D) at x = 0
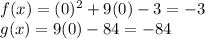
⇒ f(0) ≠ g(0)
E) at x = 9
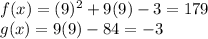
⇒ f(9) ≠ g(9)
F) at x = 9i
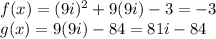
⇒ f(-9i) ≠ g(-9i)
Hence, only for x = -9i, f(x) = g(x)