Question

Two triangles are similar. The height of the smaller triangle is 6 inches and the corresponding height of the larger triangle is 15 inches. If the perimeter of the smaller triangle is 37.8 inches, what is the perimeter of the larger triangle?

Answer 1

Two triangles are similar. The perimeter of the larger triangle is 94.5 inches

SOLUTION:

Given, Two triangles are similar.

The height of the smaller triangle is 6 inches and the corresponding height of the larger triangle is 15 inches.

The perimeter of the smaller triangle is 37.8 inches,

We have to find what is the perimeter of the larger triangle?

We know that, for similar triangles, ratio of heights = ratio of perimeters

`\begin{array}{l}{\text { Then, } \frac{\text {height of } 1 \text {st triangle}}{\text {height of } 2 \text {nd} \text { triangle}}=\frac{\text {perimeter of } 1 \text {st triangle}}{\text {perimeter of } 2 n d \text { triangle}}} \\\\ {(6)/(15)=\frac{37.8}{\text { perimeter of } 2 \text {nd triangle}}}\end{array}`

`\begin{array}{l}{\text { Perimeter of } 2^{\text {nd triangle }} * 6=37.8 * 15} \\\\ {\text { Perimeter of } 2^{\text {nd triangle }}=37.8 * (15)/(6)=37.8 * (5)/(2)=(189)/(2)=94.5}\end{array}`

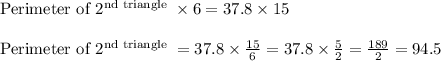
Hence, the perimeter of the larger triangle is 94.5 inches