Question

Error Degrees of Freedom are calculated as n - p - 1 for multiple regression models. The p represents the number of coefficients (not including the intercept) in the estimated model. Part A: Report the Error Degrees of Freedom for this example: Assume 160 observations are used to estimate a model with 2 numerical explanatory variables both with a linear relationship to the response and 1 categorical explanatory variable. The categorical variable has 4 levels. Part B: Assume 160 observations are used to estimate a model with 2 numerical explanatory variables both with a linear relationship to the response. In addition there is one categorical variable with 3 levels and another categorical variable with 4 levels. Report the Error Degrees of Freedom

Answer 1

Part (A) The Error Degrees of Freedom for this example is 154.

Part (B) The Error Degrees of Freedom for this example is 152.

Explanation:

Consider the provided information.

The categorical variable has 4 levels.

It is given that 160 observations are used to estimate a model with 2 numerical explanatory variables both with a linear relationship to the response and 1 categorical explanatory variable.

Thus, the total number of coefficients(p) = 2+(4-1)=5

It is given that Error Degrees of Freedom are calculated as n - p - 1

Substitute n = 160 and p=5 in above formula.

`df=160-5-1=154`

Hence, the Error Degrees of Freedom for this example is 154.

Part B: Categorical variable with 3 levels and another categorical variable with 4 levels. Also a model with 2 numerical explanatory variables both with a linear relationship to the response.

Thus, the total number of coefficients(p) = 2+(3-1)+(4-1)=7

It is given that Error Degrees of Freedom are calculated as n - p - 1

Substitute n = 160 and p=5 in above formula.

`df=160-7-1=152`

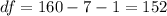
Hence, the Error Degrees of Freedom for this example is 152.