Question

A coin rests 13.0 cm from the center of a turntable. The coefficient of static friction between the coin and turntable surface is 0.440. The turntable starts from rest at t = 0 and rotates with a constant angular acceleration of 0.840 rad/s2. (a) Once the turntable starts to rotate, what force causes the centripetal acceleration when the coin is stationary relative to the turntable? Under what condition does the coin begin to move relative to the turntable?

Answer 1

(a) The turn table velocity

(b) 6.86s

Explanation:

(a) The velocity of the turntable would be the one causing centripetal acceleration on the coin and the equation for that is

`a_c = (v^2)/(r) = ((\omega r)^2)/(r) = \omega^2r = (\alphat)^2r`

Where
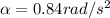`\alpha = 0.84 rad/s^2` is the angular acceleration and r = 13 cm = 0.13 m is the distance form table origin to the coin

There's also an inertia force causes by the turntable angular acceleration, this force would have its acceleration equal to:

`a_i = \alpha r`

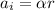
This acceleration would be perpendicular to the centripetal acceleration. So the total acceleration acting on the coin is:

`\vec{a} = \vec{a_c} + \vec{a_i}`

`a^2 = a_c^2 + a_i^2`

`a^2 = \alpha^4t^4r^2 + \alpha^2r^2`

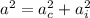
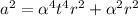
(b) The coins begins to move when its total acceleration force begin to wins its static friction force, which is generated by gravity

`F_a = F_f`

`ma = mg\mu`

`a^2 = (g\mu)^2`

`\alpha^4t^4r^2 + \alpha^2r^2 = (g\mu)^2`

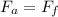
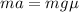
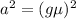
We can substitute in the known parameters (
`g = 9.81 m/s^2`)

`0.84^4*0.13^2t^4 + 0.84^2*0.13^2 = (9.81*0.44)^2`

`0.008414t^4 + 0.01192464  = 18.631`

`t^4 = 18.61938432/0.008414 = 2212.9`

`t = 2212.9^(1/4) = 6.86 s`

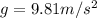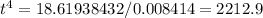
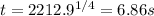
So the coin would start moving after 6.86s.