Question

(08.04 MC)

Find the sum of the geometric sequence 3, 15, 75,375, ... when there are 8 terms and select the correct answer below.

Answer 1

292,968

Explanation:

As we know,

Sum of a geometric sequence (S) =
`(a(1-r^(n)) )/((1-r))`

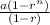
where,

a = first term of sequence,

r = the constant ratio,

n = number of terms in sequence.

So, according to the question,

a = 3,

r = 5,

n = 8.

by substituting the values in the above formula, we get;

⇒
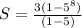
`S=(3(1-5^(8)) )/((1-5))`

⇒
`292,968`