Question

ASAP PLEASEEEEEEE!!!!!!!!!!

Answer 1

d. moving at
`3.1 m/s^2`

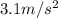
Step-by-step explanation:

We can solve the problem by applying Newton's second law:

`F=ma` (1)

where

F is the net force on the object

m is the mass of the object

a is its acceleration

Here we are only interested in the motion of the object along the horizontal direction. There are two forces acting on the object in this direction:

- The force
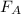`F_A`, pushing to the right, with magnitude 8.4 N

- The force
`F_f`, pulling to the left, with magnitude 2.2 N

So, we can rewrite (1) as

`F_A - F_f = ma`

Where:

`F_A = 8.4 N\\F_f = 2.2 N\\m = 2.0 kg`

And solving for a, we find the acceleration:

`a=(F_A-F_f)/(m)=(8.4-2.2)/(2.0)=3.1 m/s^2`

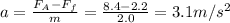
and the direction is the same as the net force, so to the right.