Question

10. A scientist throws a rock straight upwards on Mars and

it reaches a height of 55m.
a. What was the initial velocity of the rock?
| b. How long was the rock in the air for?

Answer 1

a. 20.4 m/s upward

The motion of the rock thrown upward is a free-fall motion, with a constant acceleration downward, given by

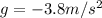`g=-3.8 m/s^2` (acceleration of gravity on Mars)

So, we can use the following suvat equation:

`v^2-u^2=2as`

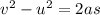
where

v is the final velocity of the rock

u is the initial velocity

a is the acceleration (
`g=-3.8 m/s^2`)

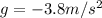s is the displacement

For the rock in the problem:

v = 0 (at the maximum height, the velocity is zero)

s = 55 m (the maximum height)

Solving for u, we find the initial velocity:

`u=√(v^2-2as)=√(0-2(-3.8)(55))=20.4 m/s`

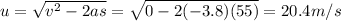
b. 10.74 s

First of all, we can find the time the rock takes to reach the maximum height, that is given by the equation

`v=u+at`

And solving for t,

`t=(v-u)/(a)=(0-20.4)/(-3.8)=5.37 s`

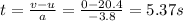
Now we notice that the motion of the rock is symmetrical, so the way down takes exactly the same as the way up: therefore, the total time of flight of the rock is

`T=2t=2(5.37)=10.74 s`