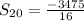The sum of first 20 arithmetic series
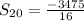
Given:
Arithmetic series for 3rd term is 55
Arithmetic series for 7th term is -98
To find:
The sum of first 20 Arithmetic series
Step by Step Explanation:
Solution:
Formula for calculating arithmetic series
Arithmetic series=a+(n-1) d
Arithmetic series for 3rd term
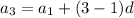
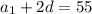
Arithmetic series for 19th term is


Subtracting equation 2 from 1
![\left[a_(19)+18 d=-98\right]+\left[a_(1)+2 d=55\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1bnudhowwmrib0dalq9m5mhk08sk75upvb.png)
16d=-98-55
16d=-153
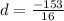
Also we know
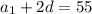
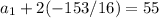
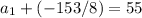
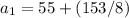
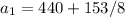
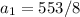
First 20 terms of an AP



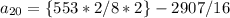
![a_(20)=[1106 / 16]-[2907 / 16]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/f7x5j0t5kw4iyhf0m9a5oueiz6z0xvf97p.png)
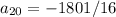
Sum of 20 Arithmetic series is
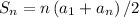
Substitute the known values in the above equation we get
![S_(20)=\left[(20\left(\left((558)/(8)\right)+\left((-1801)/(16)\right)\right))/(2)\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/c1x9ok5fbqfi0atp1fm4jjl994tlglaipx.png)
![S_(20)=\left[(\left.20\left((1106)/(16)\right)+\left((-1801)/(16)\right)\right))/(2)\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/i6n3xj63xzb1h89977puu9cjl9oc3o8bm3.png)
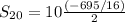
![S_(20)=5\left[(-695)/(16)\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/33aesuhgky3cxqumalokf2medrz4kbykxk.png)
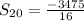
Result:
Thus the sum of first 20 terms in an arithmetic series is