Question

A square plate of side 9 m is submerged in water at an incline of 60∘ with the horizontal. Its top edge is located at the surface of the water. Calculate the fluid force F(in Newtons) on one side of the plate (assume the water weight density isW=9800 N/m3).

Answer 1

The force on one side of the plate is 3093529.3 N.

Step-by-step explanation:

Given that,

Side of square plate = 9 m

Angle = 60°

Water weight density = 9800 N/m³

Length of small strip is

`y=(\Delta y)/(\sin60)`

`y=(2\Delta y)/(√(3))`

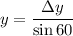
The area of strip is

`dA=(9*2\Delta y)/(√(3))`

We need to calculate the force on one side of the plate

Using formula of pressure

`P=(dF)/(dA)`

`dF=P* dA`

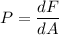
On integrating

`\int{dF}=\int_(0)^(9\sin60){\rho g* y* 6√(3)dy}`

`F=9800*6√(3)((y^2)/(2))_(0)^(9\sin60)`

`F=9800*6√(3)*(((9\sin60)^2)/(2))`

`F=3093529.3\ N`

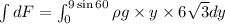
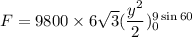
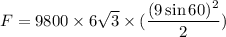
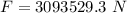
Hence, The force on one side of the plate is 3093529.3 N.