Answer:
719.84 rad/s²
Step-by-step explanation:
Given that:
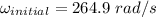
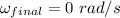 (Has to come to rest)
(Has to come to rest)
t = 0.368 seconds
Thus, the expression for angular expression is:-
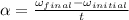
Applying the values in the above equation as:-
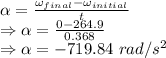
Magnitude of the average angular acceleration = 719.84 rad/s²