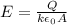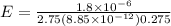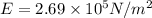Answer:
Part a)
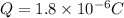
Part b)
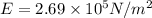
Step-by-step explanation:
Part a)
When capacitor is completely charged then its charge is given as
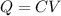
here we know that
C = 50 nF
V = 36.0 Volts
now we have
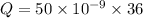
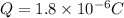
Part b)
now we know that
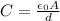
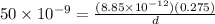
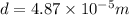
Now electric field inside the plastic sheet is given as