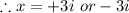Question

Which of the following expressions is equal to 3x^2+27

Answer 1

The roots of the the given equation are +3i or -3i.

Solution:

Given,
`3x^2+27=0`

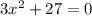
First of all compare the given equation with the standard form, i.e
`ax^2+bx+c=0`

On comparing,

a=3

b=0

c=27

According to the quadratic formula,

`x = \frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

`b^2-4ac= 0-4*3*27=-324`

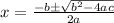
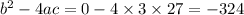
As
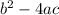`b^2-4ac` comes out to be negative, the given equation does not have any real roots,

`\sqrt {b^2-4ac}= √((-324))`

`\sqrt {b^2-4ac}= √((324* -1))`

`\Rightarrow √(324)* √(-1)`

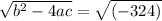
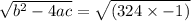
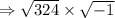
Root of 324 is 18,

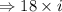`\Rightarrow 18* i` (Because root of -1 is i)

`x=((-0+-18i))/(2*3)`

`x=(\pm18i)/(6)`

`x=(+18)/(6) \ or (-18)/(6)`

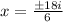
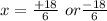
On dividing 18 and 6 we get,

`\therefore x=+3i \ or -3i`