Answer:
$454.45
Step-by-step explanation:
Given that,
Confidence interval = 90%
From the Z-table,
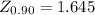
Standard deviation of weight (SD) = 0.17 pound
Sampling error of mean weight (SE) = 0.016 pound
Therefore,
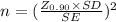
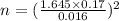
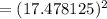
= 305.4
n ≅ 305 (approx)
Thus, the needed sample size is 305.
Budget in dollars = 305 × $1.49
= $454.45