Question

Need 100 IQ and more

A food package is dropped from a helicopter flying horizontally at a height of 125m. If the magnitude of the velocity of the packageafter 2seconds is 25m/s. Find

a. The speed of the helicopter at the moment the package is dropped.

b. The position of the package after 2s.

c. The time of flight of the food package

d. The horizontal distance covered.​

Answer 1

a. The speed of the helicopter at the moment the package is dropped is approximately 15.519 m/s

b. The position of the package 2s after it is dropped is (31.038 m, -9.8 m)

c. The time of flight of the food package is approximately 5.105 seconds

d. The horizontal distance covered is approximately 79.22 m

Step-by-step explanation:

The given parameters are;

The height at which the helicopter is flying = 125 m

The magnitude of the velocity of the package after 2 seconds, v = 25 m/s

a. The vertical velocity of the package,
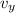`v_y`, is given as follows;

`v_y` =
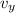`u_y` + g·t

Where;

`u_y` = 0 m/s for the dropped food package

t = The duration of the package in the air = 2 s

g = The acceleration due to gravity = 9.8 m/s²

Therefore;

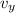`v_y` = g·t = 9.8 m/s² × 2 s = 19.6 m/s

We have,
`v = √(v_x^2 + v_y^2)`,

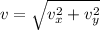Where;

vₓ = The horizontal velocity of the food package = The horizontal speed of the helicopter

therefore,
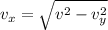`v_x = √(v^2 - v_y^2)`, which gives;

`v_x = √(v^2 - v_y^2) = √(25^2 - 19.6^2) \approx 15.519 \ m/s`

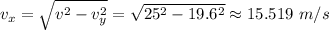
The speed of the helicopter at the moment the package is dropped ≈ 15.519 m/s

b. The vertical if the package after 2 s is given as follows;

The vertical position of the package after 2 s is given by the kinematic equation, h = 1/2·g·t² = 1/2 × 9.8 m/s² × 2 s = 9.8 m

The food package is located 9.8 m vertically below the point where it is dropped

The horizontal position, x, of the package after 2 s is given by the following kinematic equation, x = vₓ × t

Therefore, x = 15.519 m/s × 2 s ≈ 31.038 m

The coordinates of the location of the package 2 seconds after it is dropped is (31.038 m, 9.8 m)

c. The time of flight,
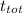`t_(tot)`, of the food package which is the time it takes the package to reach the ground from 125 m, is given as follows;

`t_(tot) = \sqrt{(2 \cdot h)/(g) } = \sqrt{(2 * 125 \ m)/(9.8 \ m/s^2) } \approx 5.051 \ seconds`

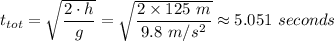
The time of flight of the food package,
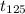`t_(125)` ≈ 5.105 seconds

d. The horizontal distance covered,
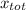`x_(tot)` = vₓ ×
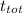`t_(tot)` ≈ 15.519 m/s × 5.105 s = 79.224495 m ≈ 79.22 m.