Question

Jack and Jill live 126 km apart. They want to leave their homes at the same time,

ride their bikes toward each other, meet for lunch at 12:00 PM, and then go climb
a hill. Jack rides 18 kilometers per hour. Jill rides 24 kilometers per hour. What is
the latest time they can leave their houses and meet on time?

Answer 1

Jack and Jill must start riding their bikes at 9:00 AM in order to travel 126 km towards each other and meet at noon, with Jack riding at 18 km/h and Jill riding at 24 km/h.

Step-by-step explanation:

To solve this problem, we need to calculate the time it would take for Jack and Jill to meet each other if they start riding towards one another from 126 km apart. Let's denote the time they need to meet at noon as 't' hours. Since Jack rides at 18 kilometers per hour and Jill rides at 24 kilometers per hour, their combined speed towards each other is 18 + 24 = 42 km/h.

The distance they need to cover before they meet is 126 kilometers. We can set up the following equation using the formula distance = speed × time:

126 km = 42 km/h × t

To find 't' we divide both sides by 42 km/h:

t = 126 km / 42 km/h

t = 3 hours

Therefore, they need to start riding 3 hours before noon to meet on time. This means the latest time they can leave their houses is 9:00 AM.

Answer 2

Both will leave their homes to meet on time at 9 am

Step-by-step explanation:

Given as, Distance between Jack and Jill = 126 km

Speed of Jack rides = 18 kilometers per hours

Speed of Jill rides = 24 kilometers per hours

Let the distance travel by Jack = x km

And the distance travel by Jill = (126 - x ) km

Time taken by Jack and Jill = T hours

Now , Distance = Speed × Time

So, x = 18 × T

And 126 - x = 24 × T

Or, 126 - x = 24 ×
`(x)/(18)`

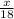
Or, 126 - x = x ×
`(4)/(3)`

Or, 378 - 3x = 4x

Or, 378 = 7x

i.e x =
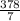`(378)/(7)` = 54 km

And distance travel by Jill = 126 - 54 = 72 km

So, time taken by Jack =
`(x)/(18)` =
`(54)/(18)`

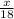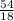
Or, Time taken by Jack = 3 hours

Similarly Time take by Jill =
`(72)/(24)` = 3 hours

∵ Both Jack and Jill will take 3 hours to meet at 12 : 00 pm

Hence, Both will leave their homes to meet on time at 9 am Answer