Answer:
F = 0.179 N
Step-by-step explanation:
given,
length of the rod = 0.759 m
mass of the rod = 1.03 kg
force = ?
initial angular speed = 0 rad/s
final angular speed = 6.87 rad/s
time interval = 9.95 s
the angular acceleration
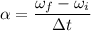

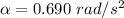
moment inertial of the rod
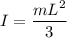
torque produced by the rod τ = I α
torque is also equal to τ = F L
now,
F L = I α
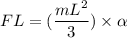
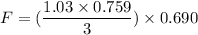
F = 0.179 N