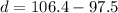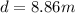Answer:
Part a)
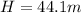
Part b)
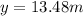
Part c)
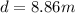
Step-by-step explanation:
Part a)
As we know that ball will reach at maximum height at
t = 3 s
now we will have
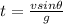
now we have
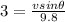
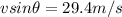
Now maximum height above ground is given as
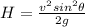
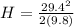
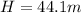
Part b)
Height of the fence is given as
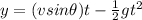
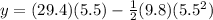
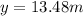
Part c)
As we know that its horizontal distance moved by the ball in 5.5 s is given as
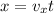
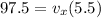

now total time of flight is given as
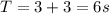
so range is given as
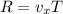
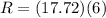
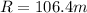
so the distance from the fence is given as