Question

The determined Wile E. Coyote is out once more to try to capture the elusive roadrunner. The coyote wears a new pair of power roller skates, which provide a constant horizontal acceleration of 15 m/s2. The coyote starts off at rest 70 m from the edge of a cliff at the instant the roadrunner zips by in the direction of the cliff. (a) If the roadrunner moves with constant speed, find the minimum speed the roadrunner must have to reach the cliff before the coyote.

Answer 1

22.91 m/s

Step-by-step explanation:

Data provided in the question:

Horizontal acceleration, a = 15 m/s²

Distance from start to cliff = 70 m

now,

Time taken to reach 70 m

from Newton's equation of motion, we have

`s=ut+(1)/(2)at^2`

here,

s is the distance

a is the acceleration

t is the time

on substituting the respective values, we get

`70=0* t+(1)/(2)*15* t^2`

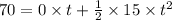
or

t² = 9.333

or

t = 3.05 s

therefore , the minimum speed =
`\frac{\textup{Distance}}{\textup{Time}}`

=
`\frac{\textup{70}}{\textup{3.05}}`

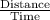
= 22.91 m/s