Question

A 50.0-kg projectile is fired at an angle of 30 degrees above thehorizontal with an initial speed of 1.20 x 102 m/s fromthe top of a cliff 142m above level ground, where the ground istaken to be y=0. a.) What is the initial total mechanicalenergy of the projectile? b.) Suppose the projectile istraveling 85.0 m/s at its maximum height of y=427m. How muchwork has been done on the projectile by air friction? c.)What is the speed of the projectile immediately before it hits theground if air friction does one and a half times as much work onthe projectile when it is going down as it did when it was goingup?

Answer 1

a) Em₀ = 42.96 104 J , b)
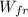`W_(fr)` = -2.49 105 J , c) vf = 3.75 m / s

Step-by-step explanation:

The mechanical energy of a body is the sum of its kinetic energy plus the potential energies it has

Em = K + U

a) Let's look for the initial mechanical energy

Em₀ = K + U

Em₀ = ½ m v2 + mg and

Em₀ = ½ 50.0 (1.20 102) 2 + 50 9.8 142

Em₀ = 36 104 + 6.96 104

Em₀ = 42.96 104 J

b) The work of the friction force is equal to the change in the mechanical energy of the body

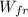`W_(fr)` = Em₂ -Em₀

Em₂ = K + U

Em₂ = ½ m v₂² + m g y₂

Em₂ = ½ 50 85 2 + 50 9.8 427

Em₂ = 180.625 + 2.09 105

Em₂ = 1,806 105 J

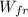`W_(fr)` = Em₂ -Em₀

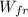`W_(fr)` = 1,806 105 - 4,296 105

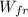`W_(fr)` = -2.49 105 J

The negative sign indicates that the work that force and displacement have opposite directions

c) In this case the work of the friction going up is already calculated in part b and the work of the friction going down would be 1.5 that job

We have that the work of friction is equal to the change of mechanical energy

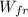`W_(fr)` = ΔEm

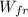`W_(fr)` = Emf - Emo

-1.5 2.49 10⁵ = ½ m vf² - 42.96 10⁴

½ m vf² = -1.5 2.49 10⁵ + 4.296 10⁵

½ 50.0 vf² = 0.561

vf = √ 0.561 25

vf = 3.75 m / s