Question

A rifle bullet with mass 8.00g strikes and embeds itself in a block with mass 0.992kg that rests on a frictionless, horizontal surface. The block is attached to a coil spring. The impact compresses the spring 15.0cm. Calibration of the spring shows that a force of 0.75N is required to compress the spring 0.25cm. Find the magnitude of the block\'s velocity just after the impact. What is the initial speed of the bullet?

Answer 1

block velocity v = 0.09186 = 9.18 10⁻² m/s and speed bollet v₀ = 11.5 m / s

Step-by-step explanation:

We will solve this problem using the concepts of the moment, let's try a system formed by the two bodies, the bullet and the block; In this system all scaffolds during the crash are internal, consequently, the moment is preserved.

Let's write the moment in two moments before the crash and after the crash, let's call the mass of the bullet (m) and the mass of the Block (M)

Before the crash

p₀ = m v₀ + 0

After the crash

`p_(f)` = (m + M) v

p₀ =
`p_(f)`

m v₀ = (m + M) v (1)

Now let's lock after the two bodies are joined, in this case the mechanical energy is conserved, write it in two moments after the crash and when you have the maximum compression of the spring

Initial

Em₀ = K = ½ m v2

Final

E
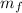`m_(f)`= Ke = ½ k x2

Emo = E
`m_(f)`

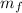
½ m v² = ½ k x²

v² = k/m x²

Let's look for the spring constant (k), with Hook's law

F = -k x

k = -F / x

k = - 0.75 / -0.25

k = 3 N / m

Let's calculate the speed

v = √(k/m) x

v = √ (3/8.00) 0.15

v = 0.09186 = 9.18 10⁻² m/s

This is the spped of the block plus bullet rsystem right after the crash

We substitute calculate in equation (1)

m v₀ = (m + M) v

v₀ = v (m + M) / m

v₀ = 0.09186 (0.008 + 0.992) /0.008

v₀ = 11.5 m / s