Answer:
Remainder is 12.
The binomial
 is not a factor of the given polynomial.
is not a factor of the given polynomial.
Explanation:
The Remainder Theorem states that when a polynomial
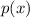 is divided by a binomial
is divided by a binomial
 , then the remainder is given as
, then the remainder is given as
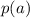 .
.
Also, if
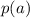 is 0, then
is 0, then
 is a factor of the given polynomial.
is a factor of the given polynomial.
Here,
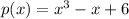 and
and
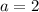
So, the remainder on dividing
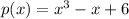 by
by
 is
is
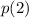 .
.
Now,
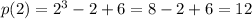 .
.
Therefore, the remainder is 12.
∵
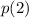 is equal to 12 and not 0. So, the binomial
is equal to 12 and not 0. So, the binomial
 is not a factor of the given polynomial.
is not a factor of the given polynomial.