Question

9. Find a polynomial of degree 4 whose coefficients are real numbers and that has

zeros -1, 2, and -2i.

Answer 1

p(x) =
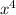`x^(4)` - x³ + 2x² - 4x - 8

Explanation:

Note that complex roots occur in conjugate pairs.

Given x = - 2i is a root then x = 2i is also a root

The roots of the polynomial are x = - 1, x = 2, x = - 2i and x = 2i

Thus the factors of the polynomial are

(x + 1), (x - 2), (x - 2i) and (x + 2i)

The polynomial is the product of it's roots, thus

p(x) = (x + 1)(x - 2)(x - 2i)(x + 2i) ← expand in pairs

= (x² - x - 2)(x² - 4i²) → note i² = - 1, so

= (x² - x - 2)(x² + 4) ← distribute parenthesis

=
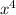`x^(4)` + 4x² - x³ - 4x - 2x² - 8 ← collect like terms

=
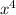`x^(4)` - x³ + 2x² - 4x - 8