1 Answer

Rewind · Answer 1 · 2020-09-09T23:34:33+0000

For this case we must solve the following system of equations:

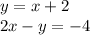
$y = x + 2\\2x-y = -4$

So, we substitute the first equation in the second one:

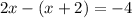
2x- (x + 2) = - 4

We consider by law of signs of multiplication that:

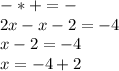
$- * + = -\\2x-x-2 = -4\\x-2 = -4\\x = -4 + 2$

Different signs are subtracted and the sign of the major is placed:

x = -2

We look for the value of the variable "y":

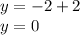
$y = -2 + 2\\y = 0$

Thus, the solution of the system is given by:
(x, y): (- 2,0)

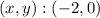
Answer:

Option B

Please log in or register to add a comment.