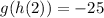For this case we have the following functions:

We must find
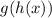 when
when
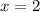 .
.
So:
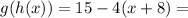
We apply distributive property to the terms within parentheses taking into account that:

We add similar terms taking into account that different signs are subtracted and the sign of the major is placed:

Thus, we have to:
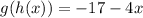
Then, with x = 2:

Equal signs are added and the same sign is placed.
Answer: