Answer:
The length of base=19cm
The length of height=13cm
Given:
Area of the triangle A=123.5
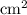
Height of the triangle h=b-6
To find:
Length of the base
Length of the height
Step by Step Explanation:
Solution:
According to the formula, Area of the triangle
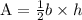
Where b=Base of the triangle
h=Height of the triangle
We know the value of A=123.5
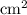 and also we know
and also we know
h=b-6
Substitute these values in the above equation we get
123.5=
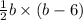
247=
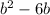
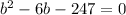
The above equation is of the form
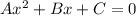
Compare the above two equations we get
A=1, B=-6, C=-247
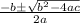
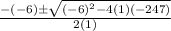
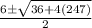
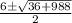
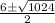
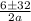
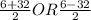
38/2 OR -26/2
The value of b can't be negative so we take
b=38/2=19cm
Though we know that
h=b-6=19-6=13cm
Result:
Thus the length values of b and h are 19 and 13 cm respectively