Question

Solve the inequality 3t+1 < t + 12​

Answer 1

`\bold{Answer:}`

`\large\boxed{t < \displaystyle(11)/(2) }`

`\bold{Solution:}`

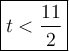
Hi!

Let's solve the inequality for t!

Our inequality is:

`\leadsto\boldsymbol{3t+1 < t+12}`

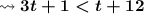
To solve it, we'll first need to subtract t from both sides:

`\leadsto\boldsymbol{2t+1 < 12}`

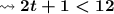
Next, subtract 1 from both sides:

`\leadsto\boldsymbol{2t < 11}`

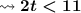
Finally, divide both sides by 2:

`\leadsto\boldsymbol{t < \displaystyle(11)/(2) }`

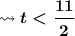
This notation indicates that all values of t which are less than 11/2 will make the inequality true.

Have a nice day!

- Stargazing ;)