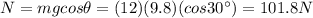Question

1. A 12kg mass is sliding down a ramp at a 30° angle from the horizontal. The coefficient of friction between the

mass and the ramp is j = 0.46.
a. What is the Normal force acting on the mass?

Answer 1

101.8 N

Step-by-step explanation:

To find the normal force acting on the mass, we just need to study the situation along the direction perpendicular to the plane.

There are only two forces acting along this direction:

- The normal force on the box, N, out of the inclined plane

- The component of the weight perpendicular to the plane, in the opposite direction, of magnitude

`mg cos \theta`

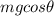
where

m = 12 kg is the mass of the object

`g=9.8 m/s^2` is the acceleration of gravity

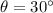`\theta=30^(\circ)` is the angle of the ramp

The mass is in equilibrium along this direction, so the equation of motion is

`N-mg cos \theta = ma = 0`

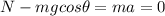
Since the acceleration is zero: a = 0.

Therefore, we can now solving the equation to find N, the normal force:

`N=mg cos \theta = (12)(9.8)(cos 30^(\circ))=101.8 N`