Question

The torque-speed curve of a 3-phase AC motor NEMA design type D can be approximated with the parabola: T=-410-5n2+0.0059n +100 where T is in Nm and n is in RPM. The motor drives the drum of a hoist (see Fig. 5-36), via a gear reducer with the reduction ratio i=60:1. Find the steady state ascending speed in m/s of a crate with mass m=1500 kg, knowing that the drum has a radius of 180 mm. Consider that:

Answer 1

The speed of the crate is 0.52m/S

Step-by-step explanation:

Hello!

The first step to solve this problem is to find the necessary torque to raise the load, for this we use the following equation

T=mgr

m=mass=1500kg

t=torque

g=gravity=9.81m/s^2

r=radius=180mm=0.18m

T=(1500)(0.18)(9.81)=2648.7Nm

the second step is to find the torque on the motor side using the reduction ratio for this we divide the torque found by 60

`T=(2648.7)/(60) =44.145Nm`

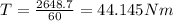
The third step is to find the turning speed with the torque speed equation and solving the quadratic equation

T=
`-4x10^-5 n^2+0.0059n+100=T\\-4x10^-5 n^2+0.0059n+100=44.145`

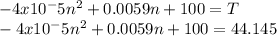
The fourth step is to solve the quadratic equation which results in N =1656.6RPM(remember take the positive solution)

the fifth step is to find the speed of rotation at the output of the speed reducer for this we divide by 60

`N=(1656.6)/(60) =27.61RPM`

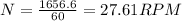
finally to find the speed of the box remember that it is the product of the speed of rotation in Rad / s by the radius in m

V=
`V=(0.18m)27.61(rev)/(min) (1min)/(60s) (2\pi )/(rev) =0.52m/S`

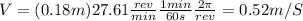
The speed of the crate is 0.52m/S