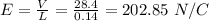Answer:
(a) I = 0.023 A
(b) J =
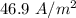
(c)
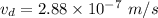
(d) E = 202.85 N/C
Solution:
As per the question:
Cross-sectional area, A =

Length of the block, L = 14.0 cm = 0.14 m
R = 1250

Potential Difference, V =
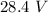
N =
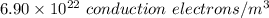
Now,
(a) Current in the block is given by:
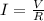

(b) Current density is given by:
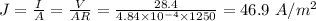
(c) Drift velocity is given by:
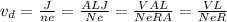
where
n =

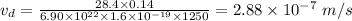
(d) The magnitude of electric field is given by: