Question

A 2.0 kg wood block is launched up a wooden ramp that is inclined at a 27 ∘ angle. The block's initial speed is 13 m/s . The coefficient of kinetic friction of wood on wood is μk=0.200. You may want to review (Page 131) . For help with math skills, you may want to review: Vector Components Part A What vertical height does the block reach above its starting point? Express your answer to two significant figures and include the appropriate units. View Available Hint(s) hh = nothing nothing Part B What speed does it have when it slides back down to its starting point? Express your answer to two significant figures and include the appropriate units. View Available Hint(s) vv = nothing nothing Provide Feedback

Answer 1

a)

`6.2` m

b)

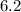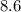`8.6` ms⁻¹

Step-by-step explanation:

`m` = mass of the wood block = 2 kg

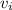`v_(i)` = initial speed of the block at the bottom = 13 m/s

`\theta` = angle of incline = 27°

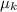`\mu _(k)` = Coefficient of kinetic friction = 0.2

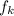`f _(k)` = kinetic frictional force

`h` = height of the incline gained

`L` = length of the incline traveled

In triangle ABC

`Sin\theta =(BC)/(AB) =(h)/(L)`

`L = (h)/(Sin \theta)`

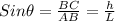
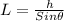
`N` = Normal force on the block by incline surface

From the force diagram of the block, force equation perpendicular to the incline surface is given as

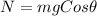`N = mg Cos\theta` Eq-1

kinetic frictional force on the block is given as

`f_(k) = \mu _(k)N`

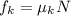
Using Eq-1

`f_(k) = \mu _(k) mg Cos\theta`

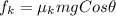
Work done by kinetic frictional force is given as

`W = f_(k) L`

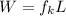
Using conservation of energy

Kinetic energy at the bottom = work done by frictional force + potential energy at the top

`(0.5) m {v_(i)}^(2) = W + mgh`

`(0.5) m {v_(i)}^(2) = f_(k) L + mgh`

`(0.5) m {v_(i)}^(2) = \mu _(k) mg Cos\theta ((h)/(Sin \theta)) + mgh`

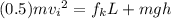
inserting the values

`(0.5) (2) (13)^(2) = (0.2) (2)(9.8) Cos27 ((h)/(Sin 27)) + (2)(9.8)h`

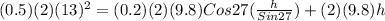
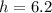`h = 6.2` m

b)

`v_(f)` = final speed of the block after returning to starting point

Using conservation of energy

Kinetic energy at the bottom initially = work done by frictional force + Kinetic energy at the bottom finally

`(0.5) m {v_(i)}^(2) = W + (0.5) m {v_(f)}^(2)`

`(0.5) m {v_(i)}^(2) = f_(k) (2L) + (0.5) m {v_(f)}^(2)`

`(0.5) m {v_(i)}^(2) = \mu _(k) mg Cos\theta ((2h)/(Sin \theta)) + (0.5) m {v_(f)}^(2)`

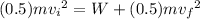
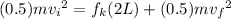
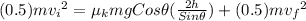
inserting the values

`(0.5) (2) (13)^(2) = (0.2) (2)(9.8) Cos27 ((2 (6.2)))/(Sin 27)) + (0.5) (2) {v_(f)}^(2)`

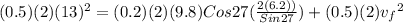
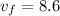`v_(f) = 8.6` ms⁻¹