Question

A bacteria culture initially contains 100 cells and grows at a

rate proportional to its size. After an hour the population has
increased to 420.
(a) Find an expression for the number of bacteria after
hours.
(b) Find the number of bacteria after 3 hours.
(c) Find the rate of growth after 3 hours.
(d) When will the population reach 10,000?

Answer 1

The required expression is:
`A=100(4.2)^t`

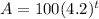
The number of bacteria after 3 hours is 7409.

The rate of growth after 3 hours is 10,632 cells per hour.

Population reach 10,000 after 3.21 hours.

Explanation:

Consider the provided information.

A bacteria culture initially contains 100 cells and grows at a rate proportional to its size.

The Continuous Exponential Growth is:

`A=A_0e^(kt)`

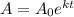
Where A₀ is the initial value, e is the exponential, k is continuous growth rate

and t is time.

Part (A) Find an expression for the number of bacteria after hours.

It is given that initial population was 100 and after an hour the population is 420.

Substitute A=420, t=1 and A₀=100 in
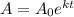`A=A_0e^(kt)` and find the growth rate as shown:

`420=100e^(k)\\4.2=e^k\\k=ln(4.2)`

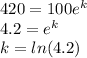
So, the required expression is:

`A=100e^(ln(4.2)t)`

`A=100(4.2)^t`

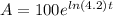
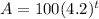
Hence, the required expression is:
`A=100(4.2)^t`

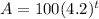
Part (B) Find the number of bacteria after 3 hours.

Substitute t=3 in above formula.

`A=100(4.2)^3`

`A=7408.8\approx7409`

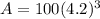
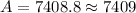
Therefore, the number of bacteria after 3 hours is 7409.

Part (C) Find the rate of growth after 3 hours.

We need to find the rate of growth after 3 hours that means if the initially number of bacteria was 7409 then what is the growth rate at time t is

`ky(t) = ln (4.2)y(t)`

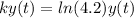
Therefore the required rate is:

`ln4.2 * 7409`

`1.43508 * 7409\approx10632.50`

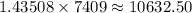
Hence, the rate of growth after 3 hours is 10,632 cells per hour

Part (D) When will the population reach 10,000?

Substitute A=10,000 in
`A=100(4.2)^t`

`10000=100(4.2)^t`

`100=(4.2)^t`

`t\approx3.21`

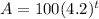
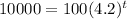
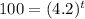
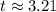
Hence, population reach 10,000 after 3.21 hours.