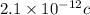Question

The membrane that surrounds a certain type of living cell has a surface area of 5.3 x 10-9 m2 and a thickness of 1.1 x 10-8 m. Assume that the membrane behaves like a parallel plate capacitor and has a dielectric constant of 5.9. (a) The potential on the outer surface of the membrane is 85.9 mV greater than that on the inside surface. How much charge resides on the outer surface?

Answer 1

The charge on the outer surface is
`2.15* 10^(- 12)\ C`

Solution:

As per the question:

Surface Area, A =
`5.3* 10^(- 9)\ m^(2)`

Thickness, t =
`1.1* 10^(- 8)\ m`

Dielectric constant, K = 5.9

Potential on the on the membrane's outer surface, V = 85.9 mV = 0.0859 V

Now,

(a) To calculate the charge on the surface, Q:

We know that the capacitance of a parallel plate capacitor can be given as:

`C = (k epsilon_(o)A)/(d)`

`C = (5.9* 8.85* 10^(- 12)* 5.3* 10^(- 9))/(1.1* 10^(- 8)) = 2.5* 10^(- 11)\ F`

`Q = CV = 2.5* 10^(- 11)* 0.0859 = 2.15* 10^(- 12)\ C`

Answer 2

`2.1* 10^(-12) c`

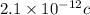
Step-by-step explanation:

We are given that

Surface area of membrane=
`5.3* 10^(-9) m^2`

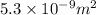
Thickness of membrane=
`1.1* 10^(-8) m`

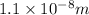
Assume that membrane behave like a parallel plate capacitor.

Dielectric constant=5.9

Potential difference between surfaces=85.9 mV

We have to find the charge resides on the outer surface of membrane.

Capacitance between parallel plate capacitor is given by

`C=(k\epsilon_0 A)/(d)`

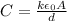
Substitute the values then we get

Capacitance between parallel plate capacitor=
`(5.9* 8.85* 10^(-12)* 5.3* 10^(-9))/(1.1* 10^(-8))`

`C=0.25* 10^(-12)F`

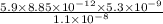
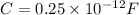
V=
`85.9 mV=85.9* 10^(-3)`

`Q=CV`

`Q=0.25* 10^(-12)* 85.9* 10^(3)=2.1* 10^(-12) c`

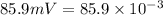
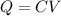
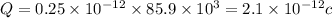
Hence, the charge resides on the outer surface=
`2.1* 10^(-12) c`