Question

A battleship simultaneously fires two shells toward two identical enemy ships. One shell hits ship A, which is close by, and the other hits ship B, which is farther away. The two shells are fired at the same speed. Assume that air resistance is negligible and that the magnitude of the acceleration due to gravity is g. Note that after Part B the question setup changes slightly. * What shape is the trajectory (graph of y vs. x) of the shells?

a.straight line
b.parabola
c.hyperbola
d. The shape cannot be determined.

Answer 1

b.parabola

Step-by-step explanation:

Lets take speed of shells = u

When they strike the enemy ships then the path followed by shells given as'

`y=xtan\theta -(gx^2)/(2u^2cos^2\theta)`

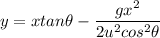
x =Horizontal distance cover by shell before striking the enemy ship

y=Vertical distance cover by shell before striking the enemy ship

θ=Angle make by initial velocity(u) from horizontal

`y=xtan\theta -(gx^2)/(2u^2cos^2\theta)`

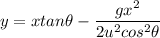
Here the power of x is 2 that is why it is the equation of parabola.

Answer is b.

b.parabola